Considere-se o circuito  série alimentado por uma fonte de tensão alternada sinusoidal cuja tensão é descrita pela expressão
série alimentado por uma fonte de tensão alternada sinusoidal cuja tensão é descrita pela expressão 

Figura 9– Esquema do circuito RL série
Conhecidos os valores de  e
e  , determinaram-se já (ver Circuito RL série) as expressões da impedância total do circuito e da corrente que ele absorve em regime permanente , considerando que a amplitude complexa da tensão tem uma fase nula na origem, isto é,
, determinaram-se já (ver Circuito RL série) as expressões da impedância total do circuito e da corrente que ele absorve em regime permanente , considerando que a amplitude complexa da tensão tem uma fase nula na origem, isto é,  .
.
 |
com |
 |
e |
 |
A potência complexa deste circuito (isto é, a potência que a fonte deverá apresentar para alimentar este circuito) será dada por

Atendendo às amplitudes complexas da tensão e da corrente, a potência complexa é dada por

Pelo que as potências activa, reactiva e aparente são:



Como  , todas estas potências assumem valores positivos.
, todas estas potências assumem valores positivos.
Conhecendo as amplitudes complexas das tensões aos terminais de cada elemento,  e
e  (ver Circuito RL série), pode calcular-se a potência de cada um dos elementos do circuito (elemento R e elemento L).
(ver Circuito RL série), pode calcular-se a potência de cada um dos elementos do circuito (elemento R e elemento L).
Sendo  , a potência complexa associada à resistência é:
, a potência complexa associada à resistência é:

Como  (ver Figura 2 de Circuito RL série), conclui-se que :
(ver Figura 2 de Circuito RL série), conclui-se que :

Isto é, a potência activa em jogo no circuito está apenas associada à presença da resistência .
Analogamente, para a bobine tem-se  . Pelo que a potência complexa associada à bobine é:
. Pelo que a potência complexa associada à bobine é:

Como  (ver Figura 2 de Circuito RL série), conclui-se que :
(ver Figura 2 de Circuito RL série), conclui-se que :

Isto é, a potência reactiva em jogo no circuito está apenas associada à presença da bobine .
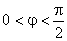 , isto é, a impedância complexa é representada por um vector no 1º Quadrante, a potência reactiva assume valores positivos ; o circuito consome energia reactiva da fonte de tensão.
, isto é, a impedância complexa é representada por um vector no 1º Quadrante, a potência reactiva assume valores positivos ; o circuito consome energia reactiva da fonte de tensão.