Considere-se o circuito 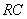 série alimentado por uma fonte de tensão alternada sinusoidal cuja tensão é descrita pela expressão
série alimentado por uma fonte de tensão alternada sinusoidal cuja tensão é descrita pela expressão 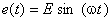
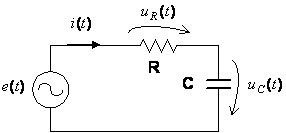
Figura 4 – Esquema do circuito RC série
Conhecidos os valores de 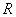 e
e 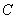 , pretende determinar-se o regime permanente da evolução temporal da corrente no circuito,
, pretende determinar-se o regime permanente da evolução temporal da corrente no circuito, 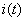 , e das tensões aos terminais da resistência,
, e das tensões aos terminais da resistência, 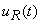 , e da capacidade,
, e da capacidade, 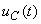 .
.
Através da Lei das Malhas, a soma da tensão aos terminais da resistência, com a tensão aos terminais da capacidade, igualará a tensão da fonte:
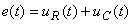
Em termos de amplitudes complexas a expressão anterior escreve-se:
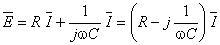
onde 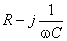 representa a impedância complexa da resistência em série com o condensador.
representa a impedância complexa da resistência em série com o condensador.
Explicitando 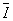 na expressão anterior, obtém-se:
na expressão anterior, obtém-se:
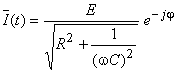 |
com |
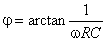 |
e |
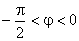 |
O diagrama vectorial das impedâncias, e amplitudes complexas da tensão da fonte e corrente, está representado na figura seguinte.
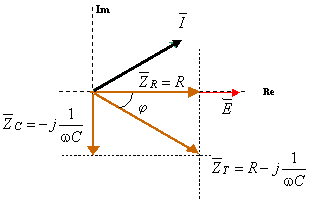
Figura 5 – Diagrama vectorial
Uma vez determinada a corrente, é imediato o cálculo das tensões aos terminais dos elementos:
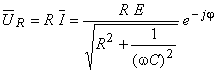
A amplitude complexa 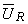 é colinear com
é colinear com 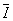 , isto é, tensão e corrente aos terminais da resistência, estão em fase.
, isto é, tensão e corrente aos terminais da resistência, estão em fase.
Relativamente à tensão aos terminais da capacidade, tem-se:
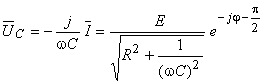
A amplitude complexa 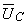 está atrasada
está atrasada 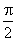 relativamente
relativamente 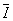 , isto é, tensão aos terminais da capacidade está atrasada
, isto é, tensão aos terminais da capacidade está atrasada 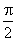 relativamente à corrente que a percorre.
relativamente à corrente que a percorre.
O diagrama vectorial completo das tensões e corrente do circuito, encontra-se representado na figura seguinte, onde se evidenciou a lei das Malhas: a soma dos vectores 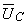 e
e 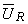 iguala o vector
iguala o vector 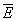 .
.
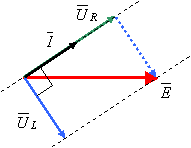
Figura 6 – Diagrama vectorial do circuito RC série
Para se obterem as expressões das evoluções temporais das grandezas há que determinar os respectivos vectores girantes (multiplicação das amplitudes complexas por 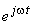 ) e fazer a sua projecção sobre o eixo dos imaginários.
) e fazer a sua projecção sobre o eixo dos imaginários.
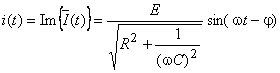

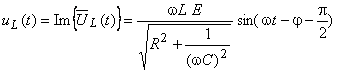
com |
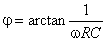 |
e |
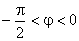 |
As expressões que foram deduzidas admitiram que a tensão que alimenta o circuito tem uma fase inicial nula. Como exercício, poder-se-á resolver o mesmo circuito RC série, admitindo que é a corrente no circuito que tem uma fase inicial nula, isto é 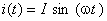 representada pela amplitude complexa
representada pela amplitude complexa 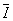 .
.
A amplitude complexa 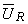 representando a tensão aos terminais da resistência é colinear com
representando a tensão aos terminais da resistência é colinear com 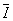 , isto é, tensão e corrente aos terminais da resistência, estão em fase.
, isto é, tensão e corrente aos terminais da resistência, estão em fase.
Relativamente à amplitude complexa 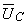 , representativa da tensão aos terminais da capacidade, está atrasada
, representativa da tensão aos terminais da capacidade, está atrasada 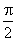 relativamente
relativamente 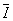 , isto é, a tensão aos terminais da capacidade está atrasada
, isto é, a tensão aos terminais da capacidade está atrasada 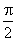 relativamente à corrente que a percorre.
relativamente à corrente que a percorre.
Finalmente, os diagramas vectorial e temporal que se obtêm são perfeitamente equivalentes aos obtidos quando se considera a tensão de alimentação com fase inicial nula; apenas diferem no instante a que se referem.