A Lei das Malhas determina que, em qualquer instante, é nula a soma algébrica das tensões ao longo de qualquer malha.

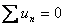
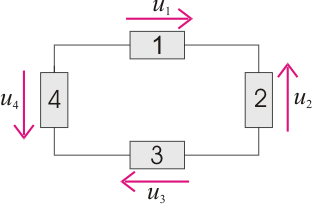
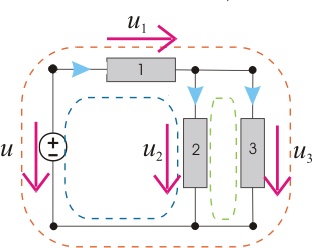
Figura 6 – Esquema representativo da Lei das Malhas

De acordo com o sentido de referência das tensões representadas na figura anterior e circulando no sentido dos ponteiros do relógio, a lei das malhas permite obter a equação:

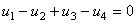
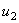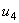Note-se que se considerou o simétrico das tensões e uma vez que o seu sentido de referência representado é o oposto ao de circulação. Não é determinante escolher o sentido horário ou o anti-horário, pois as equações obtidas de uma ou outra forma são exactamente equivalentes.

Figura 7 – Malhas do circuito

O somatório das tensões ao longo da malha ser nulo, equivale a dizer que é nulo o trabalho necessário para deslocar uma carga ao longo da malha fechada. Isto acontece porque o sistema é conservativo.

Relativamente ao circuito representado na figura 7, a aplicação da Lei das Malhas conduz a:

• Na malha vermelha e circulando no sentido horário
• Na malha azul e circulando no sentido horário
• Na malha verde e circulando no sentido horário

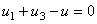
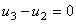
Das 3 equações representadas, apenas duas são linearmente independentes.

Existindo M malhas no circuito, a Lei das Malhas permite escrever 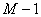equações linearmente independentes

A última equação permite afirmar que a tensão aos terminais do elemento 2 é igual à tensão aos terminais do elemento 3; por outras palavras, os dois elementos apresentam a mesma tensão aos seus terminais. Nesta situação, diz-se que os dois elementos estão ligados em paralelo.