Supor que a bobine está concentrada, equivale a admitir que todos os seus condutores se localizam em 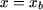 (figura 6). O teorema de Ampère aplicado a todo o contorno que atravesse o entreferro sem incluir a bobine (contorno 1 a vermelho na figura 6, atravessando o entreferro em (figura 6). O teorema de Ampère aplicado a todo o contorno que atravesse o entreferro sem incluir a bobine (contorno 1 a vermelho na figura 6, atravessando o entreferro em 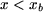 ) conduz a: ) conduz a:
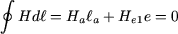 |
(21) |
O teorema de Ampère aplicado a um contorno que atravesse o entreferro e inclua a bobine (contorno 2 a preto na figura 6, atravessando o entreferro em 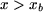 ) conduz a: ) conduz a:
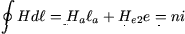 |
(22) |
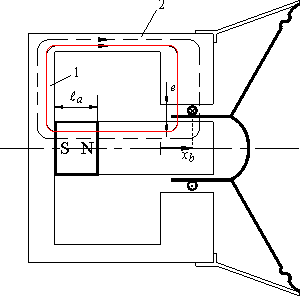
Figura 6
Para obter o valor de 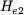 , e tal como se efectuou no caso do cálculo do campo devido ao íman, deve-se utilizar a noção de conservação do fluxo isto é, admitir como nula a dispersão: , e tal como se efectuou no caso do cálculo do campo devido ao íman, deve-se utilizar a noção de conservação do fluxo isto é, admitir como nula a dispersão:
- o fluxo através do entreferro é:
- o fluxo através do íman é:
Igualando os dois fluxos:
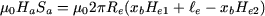 |
(23) |
Combinando as equações (21), (22) e (23), obtém-se a expressão do campo 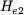 : :
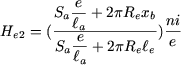 |
(24) |
O fluxo interceptado pela bobine é igual a  vezes o fluxo que atravessa o entreferro de vezes o fluxo que atravessa o entreferro de 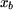 a a 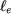
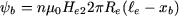 |
(25) |
Obtém-se, atendendo a (24)
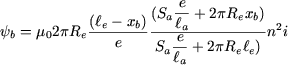 |
(26) |
A expressão para a indutância 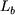 da bobine será, então: da bobine será, então:
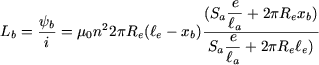 |
(27) |
A força relutante que se exerce sobre a bobine virá:
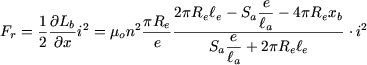 |
(28) |
Num dispositivo correctamente dimensionado, esta força, responsável pelo termo não linear na expressão que relaciona a força total que se exerce na bobine móvel à corrente que nela circula é, geralmente, negligenciável face à força de origem electrodinâmica. É por esta razão que, geralmente, só se toma em linha de conta o termo de origem electrodinâmica.
|