Impedância da resistência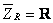

Impedância da bobine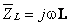

Impedância do condensador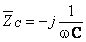

Como estas 3 impedâncias estão em série:

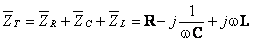, ou seja,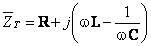

Dependendo do valor da parte imaginária da impedância, podem acontecer 3 casos:

1º Caso

A parte imaginária da impedância é nula, 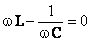, e, portanto a impedância total é puramente resistiva, .

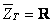O diagrama vectorial da tensão que alimenta o circuito, da corrente que o percorre e da impedância total toma a forma:

Relativamente aos terminais do circuito, trata-se de um circuito com carácter Resistivo

 

2º Caso

A parte imaginária da impedância é positiva, 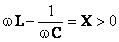, e, portanto a impedância total é resistiva e indutiva,.

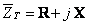O diagrama vectorial da tensão que alimenta o circuito, da corrente que o percorre e da impedância total toma a forma:

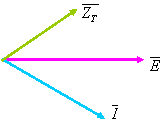
Relativamente aos terminais do circuito, trata-se de um circuito com carácter resistivo e Indutivo

 

3º Caso

A parte imaginária da impedância é negativa, 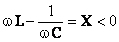, e, portanto a impedância total é resistiva e capacitiva,.

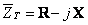O diagrama vectorial da tensão que alimenta o circuito, da corrente que o percorre e da impedância total toma a forma:

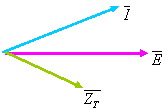
Relativamente aos terminais do circuito, trata-se de um circuito com carácter resistivo e Capacitivo

No caso concreto do problema, substituindo os valores: 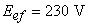, , 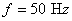, 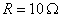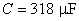e 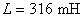, obtém-se:

Para o módulo da impedância total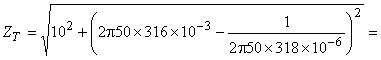

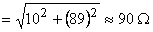
e para a fase da impedância total: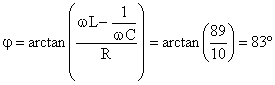

A impedância total complexa será então:

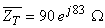
A amplitude complexa (em valor eficaz) da corrente é:

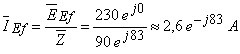
A amplitude complexa (em valor eficaz) da tensão aos terminais da resistência é:

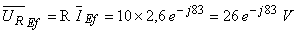
A amplitude complexa (em valor eficaz) da tensão aos terminais da indutância é:

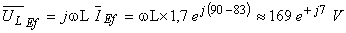
A amplitude complexa (em valor eficaz) da tensão aos terminais da capacidade é:

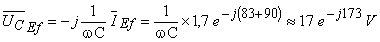
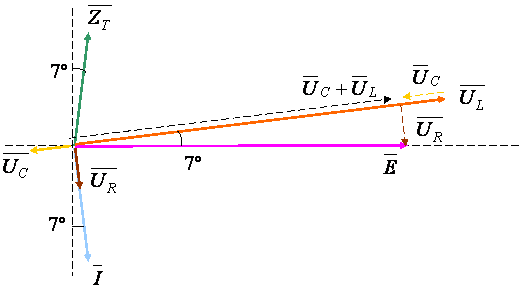
A representação vectorial destas grandezas é a representada na figura seguinte, onde evidenciou a relação existente entre as tensões do circuito (Lei das Malhas)