RESISTÊNCIA

Considere-se uma resistência cujos sentidos de referência para a tensão e corrente se encontram representados na figura seguinte.

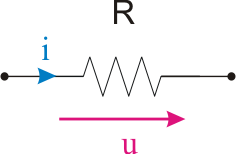
Admitindo que a corrente que percorre a resistência é alternada sinusoidal representada pela expressão:

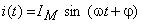
através da equação característica da resistência, 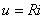é possível determinar a tensão aos seus terminais:

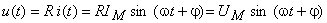
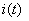A tensão aos terminais da resistência também é uma grandeza alternada sinusoidal de frequência angular , está em fase com e apresenta uma amplitude dada por .

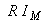Em notação complexa, o vector girante representativo de 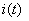é:

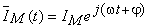
e, através da equação característica, o vector girante da tensão, 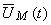será:

O vector girante da tensão apresenta a mesma frequência angular de e é colinear com este; obtém-se 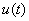fazendo a projecção deste vector sobre o eixo dos Imaginários.

Numa resistência, a tensão aos seus terminais e a corrente que a percorre estão em fase.

A figura seguinte representa a evolução temporal e o diagrama vectorial da tensão e corrente aos terminais da resistência.

 

INDUTÂNCIA

Considere-se uma indutância cujos sentidos de referência para a tensão e a corrente se encontram representados na figura seguinte.

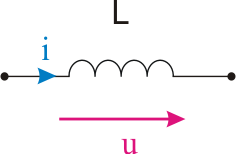
Admitindo que a corrente que percorre a indutância é alternada sinusoidal representada pela expressão:

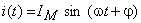
através da equação característica da indutância, é possível determinar a tensão aos seus terminais:

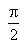A tensão aos terminais da indutância também é uma grandeza alternada sinusoidal de frequência angular , está avançada relativamente 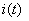e apresenta uma amplitude de .

Em notação complexa, o vector girante representativo de 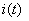é:

e, através da equação característica, o vector girante da tensão, será:

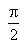O vector girante da tensão apresenta a mesma frequência angular de e está avançado relativamente a este; obtém-se 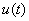fazendo a projecção deste vector sobre o eixo dos Imaginários.

 

A figura seguinte representa a evolução temporal e o diagrama vectorial da tensão e corrente aos terminais da indutância.

 

CAPACIDADE

Considere-se uma capacidade cujos sentidos de referência para a tensão e corrente se encontram representados na figura seguinte.

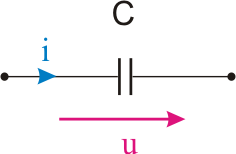
Admitindo que a corrente que percorre a indutância é alternada sinusoidal representada pela expressão:

através da equação característica da capacidade, 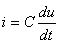é possível determinar a tensão aos seus terminais:

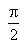A tensão aos terminais da capacidade também é uma grandeza alternada sinusoidal de frequência angular , está atrasada relativamente 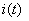e apresenta uma amplitude de .

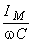Em notação complexa, o vector girante representativo de 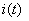é:

e, através da equação característica, o vector girante da tensão, 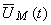será:

O vector girante da tensão apresenta a mesma frequência angular de e está atrasado 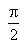relativamente a este; obtém-se 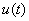fazendo a projecção deste vector sobre o eixo dos Imaginários.

A figura seguinte representa a evolução temporal e o diagrama vectorial da tensão e corrente aos terminais da capacidade.