Se o raio interior 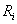e o raio exterior 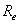do núcleo toroidal têm valores muito próximos (o que equivale a dizer que a dimensão das espiras é muito reduzida face ao raio médio, 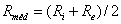, pode admitir-se, sem grande erro, que todos os contornos de integração situados no interior do núcleo toroidal têm todos, aproximadamente, o mesmo comprimento .

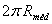Esta hipótese permite admitir que o campo de indução magnética é praticamente constante em todos os pontos de uma secção circular do núcleo (secção perpendicular ao núcleo). Como, por outro lado, o campo de indução 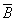é perpendicular em todos os pontos desta secção (porque é tangente ao contorno de integração), o fluxo 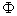através de uma secção circular do núcleo, vale, aproximadamente:

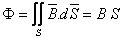(4)

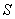onde representa a secção perpendicular ao núcleo (secção de forma circular) .

Combinando (2) e (4), obtém-se:

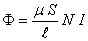(5)

sendo

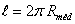
Designa-se  :

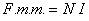• a força magnetomotriz que se exprime em Ampère-espira (Ae) ;
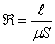• a relutância magnética do circuito magnético que se exprime em Ampère-espira por Weber (Ae/Wb)

o que permite reescrever (5) sob a forma  :

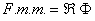(6)

Esta expressão é conhecida como Lei de Hopkinson.