Fazendo uso das amplitudes complexas da tensão e corrente de um dipolo, define-se potência complexa , 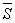 , o produto da amplitude complexa eficaz da tensão pelo conjugado da amplitude complexa eficaz da corrente.
, o produto da amplitude complexa eficaz da tensão pelo conjugado da amplitude complexa eficaz da corrente.
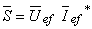
onde 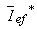 representa o complexo conjugado de
representa o complexo conjugado de 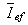 .
.
Sendo as amplitudes complexas:
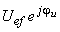 |
e |
 |
A potência complexa pode ser escrita na forma:
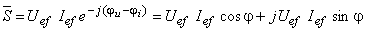
onde
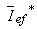
É possível identificar na expressão anterior, a potência activa (ou real), 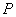 , definida na secção anterior;
, definida na secção anterior;
por analogia, define-se a potência reactiva (ou imaginária) e representa-se por 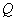 :
:
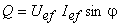
A potência reactiva expressa-se em volt ampere reactivo [var].
A potência complexa pode, então, ser reescrita na forma:
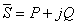
e representada graficamente pelo designado triângulo de potências , representado na figura seguinte.
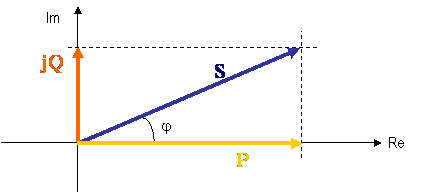
Figura 2 – Triângulo de potências
Saliente-se que tanto a potência activa 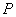 , quanto a potência reactiva
, quanto a potência reactiva 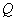 , assumem valores reais; apenas a potência complexa assume valores no conjunto dos números complexos.
, assumem valores reais; apenas a potência complexa assume valores no conjunto dos números complexos.
Os vectores que representam as potências activa, reactiva e complexa não são vectores girantes pois a sua evolução no tempo não é sinusoidal; para uma dada corrente e tensão sinusoidais (que podem ser representadas por vectores girantes), as potências activa, reactiva e complexa assumem valores constantes (que não são representadas por vectores girantes).
O módulo da potência complexa, 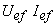 , designa-se por potência aparente , representa-se por
, designa-se por potência aparente , representa-se por 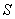 e expressa-se em volt ampere [VA].
e expressa-se em volt ampere [VA].
O factor de potência , 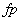 , é definido como a razão entre a potência activa e a potência aparente.
, é definido como a razão entre a potência activa e a potência aparente.
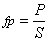
O factor de potência é uma grandeza adimensional e, apenas no caso de regimes sinusoidais, o seu valor é numericamente idêntico a  .
.
A tabela seguinte resume algumas expressões relativas às grandezas definidas nesta secção.
Potência Complexa |
|
|
- |
- |
Potência Aparente |
|
|
volt ampere |
[VA] |
Potência Activa |
|
|
watt |
[W] |
Potência Reactiva |
|
|
volt ampere reactivo |
[var] |
Factor de Potência |
|
|
- |
- |